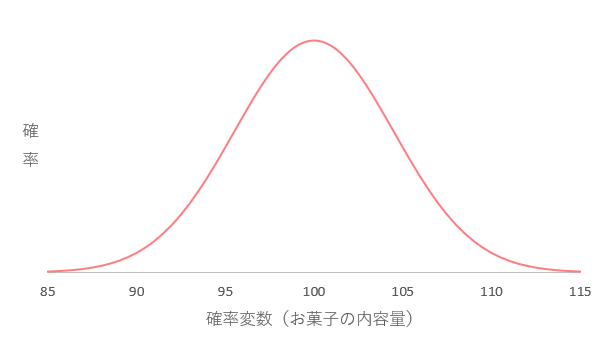
確率変数と確率分布 どのような値を取るかが確率的に決まる変数のことを 確率変数 と呼びます。確率分布関数 は、確率変数がある値を取る確率の分布を表したものです。 具体的には、確率分布関数は 確率密度関数 の積分で定義されます。 確率変数 が確率分布関数 に従うことを と表記しIt may be any set a set of real numbers, a set of vectors, a set of arbitrary nonnumerical values, etcFor example, the sample space of a coin flip would be Ω確率分布のまとめ こんにちは。 産婦人科医で人工知能の研究をしているTommy(Twitter: @obgyntommy )です。 今回の記事はベイズ統計学では様々な確率分布を用いる場合が多いです。 ベイズ統計の理論と方法の基本的内容については以下の記事を参照
離散型 連続型確率分布 Ssk Communications
確率分布 期待値
確率分布 期待値-ポアソン分布の確率関数を使って、例題を解いていきます。 ポアソン分布の確率関数 特定の期間に平均\(\lambda\)回起こる事象が、ちょうど\(k\)回起こる確率は \(P(X = k) = \frac{\lambda^k e^{\lambda}}{k!}\) \(e\)はオイラー数またはネイピア数と呼ばれています。その値は\(2718 \dots\)と続く超越数です。 「Excel(エクセル)で確率分布関数ってどう使うの?」 「二項分布、ポアソン分布、正規分布って何?」 データの分析や活用って年々重要になっています。 データを扱う上で求められることは以下の3つ。 データを入手したときにどのような集計・分析を行うべきかを検討できるデータ分



年に一度 のリスク 確率分布が 正規分布ではなかったら どうなるか ニッセイ基礎研究所
出目 場合の数 出目の確率 以上が出る確率 以下が出る確率; 統計検定の問題を問題を解くだけでなく、本質的な理解も同時に行えるようにしようという意図のシリーズです。#14では自己回帰(AR)モデルと移動平均モデル(MA)について確認しました。 #15では確率分布と確率母関数(Probability generating function)について取り扱います。ガチャの確率分布の計算(連続ガチャ用) ガチャの期待値の計算(一般のガチャ用) ガチャの期待値の計算(リセマラ用) ガチャの期待値の計算(天井付きガチャ用) ガチャの期待値の計算(排出率の異なるコンプガチャ用) ガチャの期待値の計算
3 1 046% % 046%確率分布の基本を分かりやすく解説片手間ブログ QC検定3級における正規分布の「たった一つの攻略法」とは? 確率分布の基本を分かりやすく解説 皆さんはデータのばらつきを視認するとしたらどのような方法で試みますか? ばらつきをより分かり 離散 ベータ分布 視聴率調査や、復元抽出時の不良品検査等で利用される 幾何分布 コイントスで初めて表 (成功)がでるまでの試行数の確率 離散 無記憶性を持つ唯一の離散確率分布 超幾何分布 コイントスをした複数の人の何人かに表裏の結果を尋ねた
一様分布 確率変数 \(X\) が、連続標本空間 \(l\leq X\leq u\) を持ち、その確率密度関数が標本空間にわたり一定で \ f\left( x\right) =\frac{1}{ul} \ の形をとるものを一様分布と呼ぶ。 確率変数 \(X\) が下限 \(l\) 、上限 \(u\) の一様分布に従うことを \(X\sim U\leftl,u\right\) と表す。 。分布関数は次の通りであ 二項分布 成功確率がpであるベルヌーイ試行を独立にn回行い、成功回数を確率変数Xとする分布を二項分布と言います。二項分布におけるn=1の場合がベルヌーイ分布となります。 確率変数Xが二項分布に従う時、nとpの2つの値(分布を特徴づける値「パラメーター」である)によって決まるため B 確率分布 これまで「分布」という言葉が何度も出てきたが、この「分布」とは確率分布のことを指している。 ここでは具体的なさまざまな確率分布を紹介する。 まず確率分布の定義であるが、確率分布とは、確率変数の各々の値に対する、その生起し



Matlab Note 統計 確率分布 Miyazawa S Pukiwiki



確率分布 確率変数とは 公式や求め方をわかりやすく解説 受験辞典
In this playlist we continue Statistics 101 by learning the basics of Continuous Probability Distributions We learn about the uniform, normal, t distributio 当初は確率分布について扱おうと思っていたのですがかなり長くなってしまったので今回は基礎編とします。 以下の単語が説明できる際は不要です。 ・確率密度関数(式の追加) ・累積分布関数(式の追加と説明の更新) ・確率変数 ・歪度と尖度 ・確率変数の期待値と分散(追記) またこの記正規分布 == 確率変数と確率分布 == 確率分布表とは 確率分布表とは,大雑把にいえば度数分布表の度数をその総数で割って相対度数分布表に直したものですが,詳しく言えばそれだけではありません. 例えば,次の例1表1において各人数を総人数 N=100 で



11 5 連続型確率分布と確率1 統計学の時間 統計web



統計学入門 付録
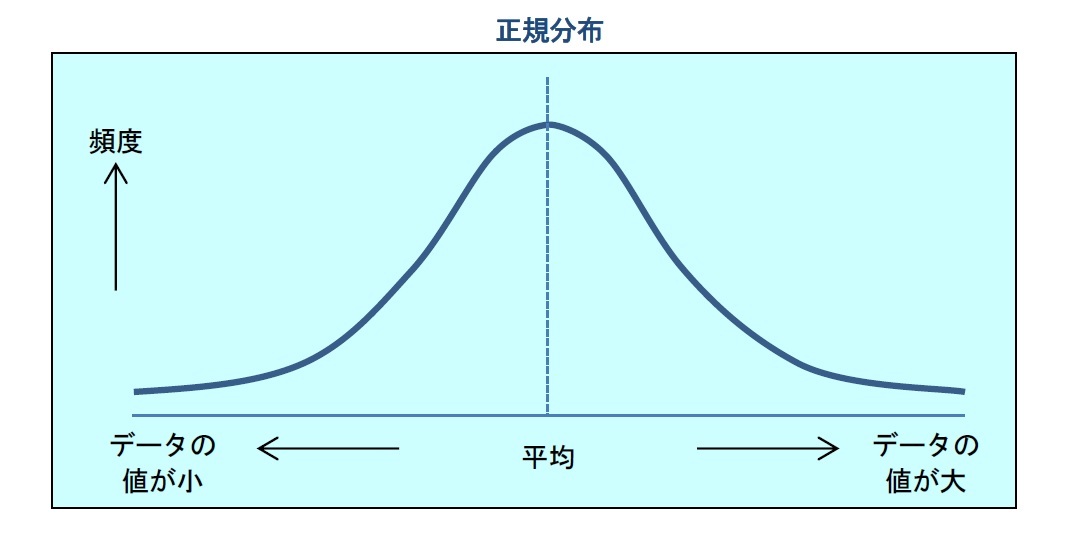
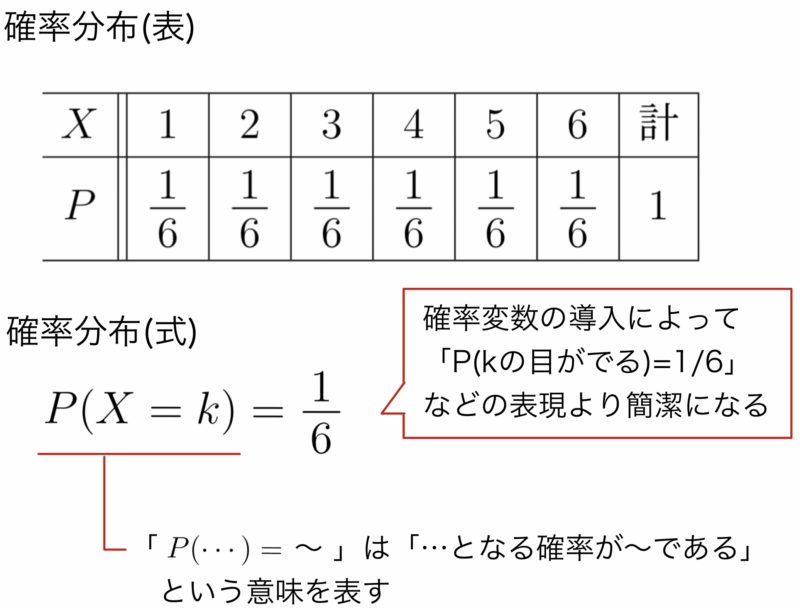
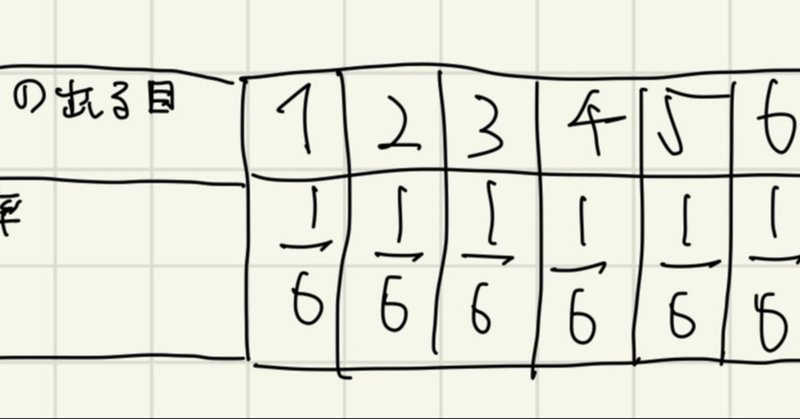
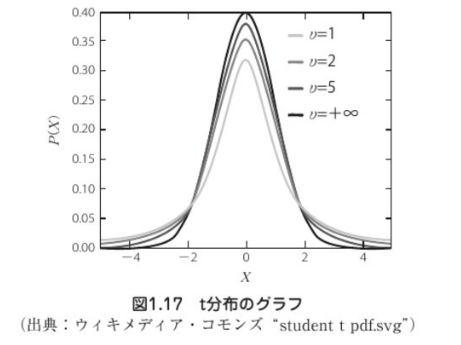
正規分布とは 正規分布とは、データが平均値付近に集まって、平均値を境に左右対称にばらついた分布です。 正規分布は、統計学において最も重要な確率分布の1つです。 なぜなら、多くの統計的手法は「データが正規分布に従うこと」が前提として考えT分布の定義 n個の確率変数 がすべて独立で、同じ正規分布 に従う時、 この確率変数 の平均を 、分散を とし、 確率変数Tを と定義すると、 この確率変数Tは自由度 のt分布に従う。 ※標本分散 に関しては「統計学の基礎」で詳しく解説します。 確率変数Tが自由度n1のt分布に従うことを以下確率分布 確率分布とは 今日は、記述統計学と統計的推測の中間的な話をします。 特に、確率に関する専門用語を定義します。 サイコロの目のように、確率的に決まる変数を、 確率変数 ( random variable )と呼びます。



統計学入門 付録



正規分布
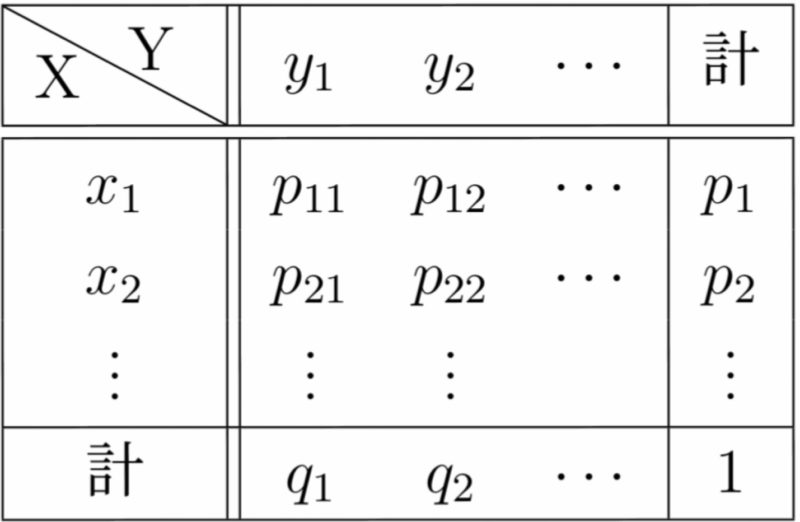
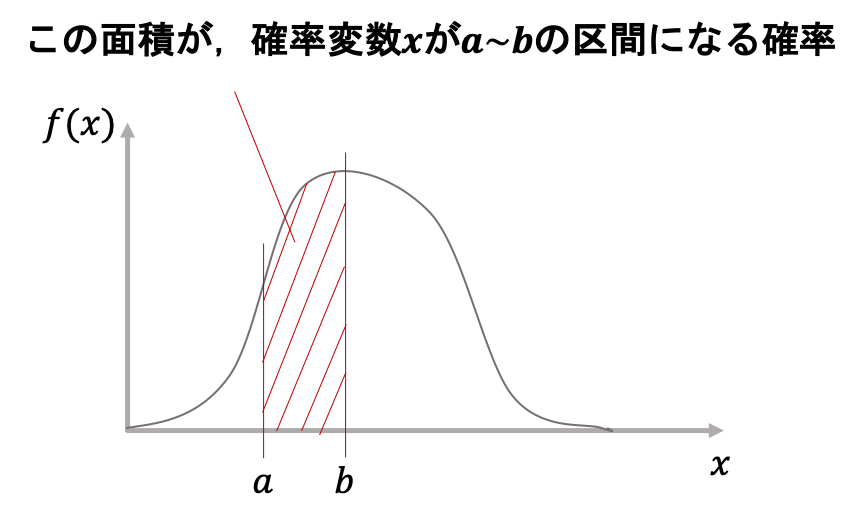
確率分布の数式的にも、連続型のほうが厳しい面をしているものが多いです。 確率分布の式が何を表しているのかわかりにくい 確率分布とは、実現値を代入するとその実現値が起きる確率を返す関数です。 関数なんです。周辺確率分布 ある確率変数 , について = , y= が同時に成り立つ確 率を, ( , )と書くこれをx,yの同時確率密度関数と呼ぶ , r0 , ∞ −∞ ∞ −∞ =1 確率変数それぞれの分布は以下のようになるこの分布を周辺 確率分布と呼ぶ = , ∞ −∞確率密度は上記の図で言うと、面積の高さに相当します。 高さである確率密度に、横幅である確率変数の範囲をかけて面積を求めることでようやく確率になります。 確率変数の幅というのは、以前に正規分布のところで出てきました。 これですね。




年に一度 のリスク 確率分布が 正規分布ではなかったら どうなるか ニッセイ基礎研究所



1
第 章 確率論の基礎 0 02 04 06 08 1 12 0 5 10 15 25 30 35 40 F x x 図 気温の確率分布関数 f Z X x dx 確率密度関数の例を挙げる。Rに用意されている確率分布 R では以下の理論分布が用意されている.ただし,スチューデント化された分布は qtukey (確率点) と ptukey (累積分布) を求める関数のみ,多項分布は dmultinom(確率密度)と rmultinom(乱数)のみ,誕生日問題の分布(近似解)は pbirthday(一致確率)と qbirthday(一致 確率分布(かくりつぶんぷ、英 probability distribution)は、確率変数に対して、各々の値をとる確率を表したものである。日本工業規格では、「確率変数がある値となる確率,又はある集合に属する確率を与える関数」と定義している。 ウィキペディア(Wikipedia)




尖度とは 定義と意味を徹底解説 初心者からはじめる統計学



1
VX = np(1 p) 証明 教科書とは違う証明を与える.示すべきことは EX = ∑n r=0 rnCrp r(1 p)n r = np で5 F 分布 2 2 1 1 ~ n 分布, 2 2 2 2 ~ n 分布で独立なとき、 1, 2 2 2 2 1 2 1 ~ n Fn n n F 分布 (自由度n1, n2 のF 分布) t 分布 X ~ N(0,1)分布, 2 ~ 2 n 分布で独立なとき、 tn n X t ~ 2 分布(自由度n のt 分布) 注)t F1,n 2 ~ 分布 注)n でN(0,1)分布 図231 確率密度関数 以下の問題は分布の統計値と確率二項分布,幾何分布の平均と分散を計算する. 二項分布の平均,分散 命題14 X が二項分布B(n;p)に従う確率変数のとき,平均と分散は次で与えられる: EX = np;
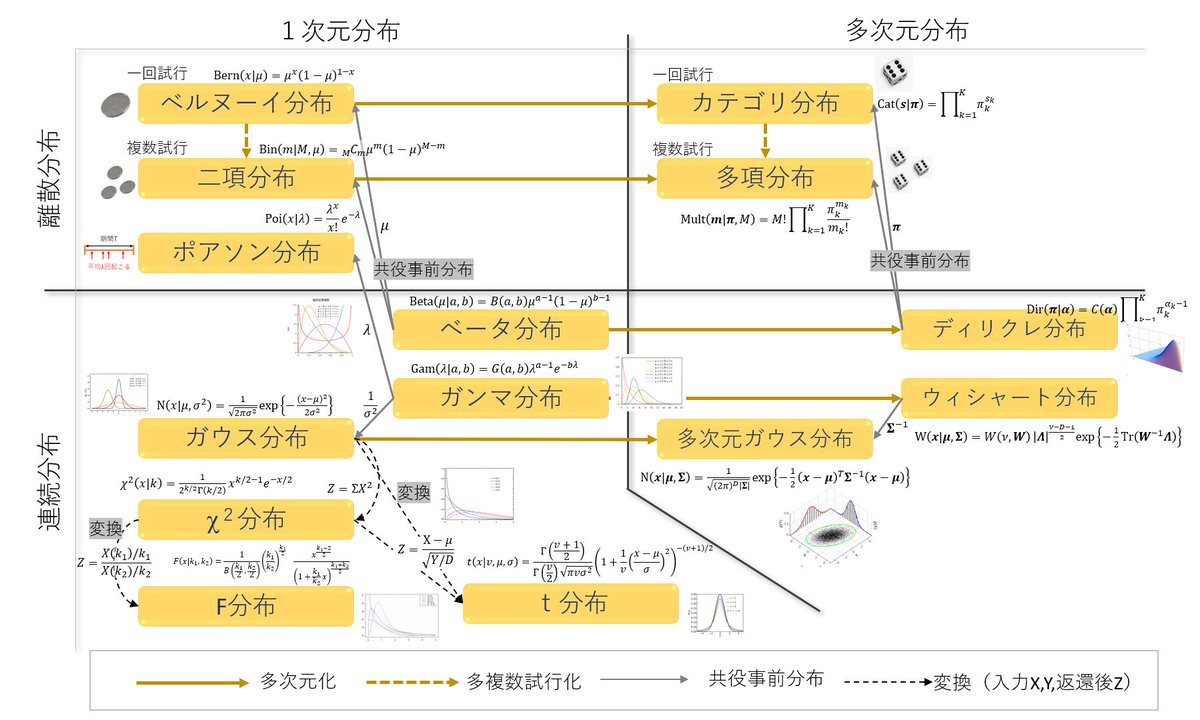



Mkt 確率分布を図のようにまとめたら理解が深まりました



確率変数 統計ブログ
今回は負の2項分布です。負の二項係数や項別微分がやや複雑だなと思いましたが、納得できるとすっきりします。 目次です。 負の2項分布とは 確率関数 確率母関数 期待値 分散 参考図書 負の2項分布とは 成功確率をとした時の、回成功するまでの失敗回数についての確率分布です。 確率分布を比較する では、確率変数で「確率による重み」をつけて計算するとどんなメリットがあるのか。 その答えとしては ① リスク・リターンのバランス を考えた選択ができるようになる ②いま起きたことが 偶然とは考えにくい現象かどうか判断Probability Distributions Viewer Toggle navigation Bookmark




確率分布 分散の計算公式の使い方 数学b 定期テスト対策サイト




離散型の確率変数とは 離散確率分布と確率関数の性質 アタリマエ
A probability distribution is a mathematical description of the probabilities of events, subsets of the sample spaceThe sample space, often denoted by , is the set of all possible outcomes of a random phenomenon being observed;




確率密度関数とは 読書の人気 最新記事を集めました はてな




確率分布 澤山 晋太郎 数学 Kindleストア Amazon



R Source
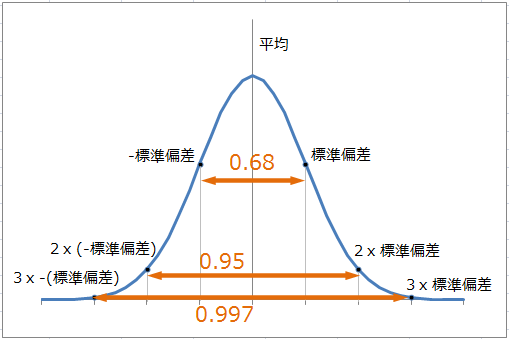



情報処理 第5回 連続確率分布




平均年収の分布から対数正規分布と確率分布 確率変数について学ぼう 20代サラリーマンの全方位投資
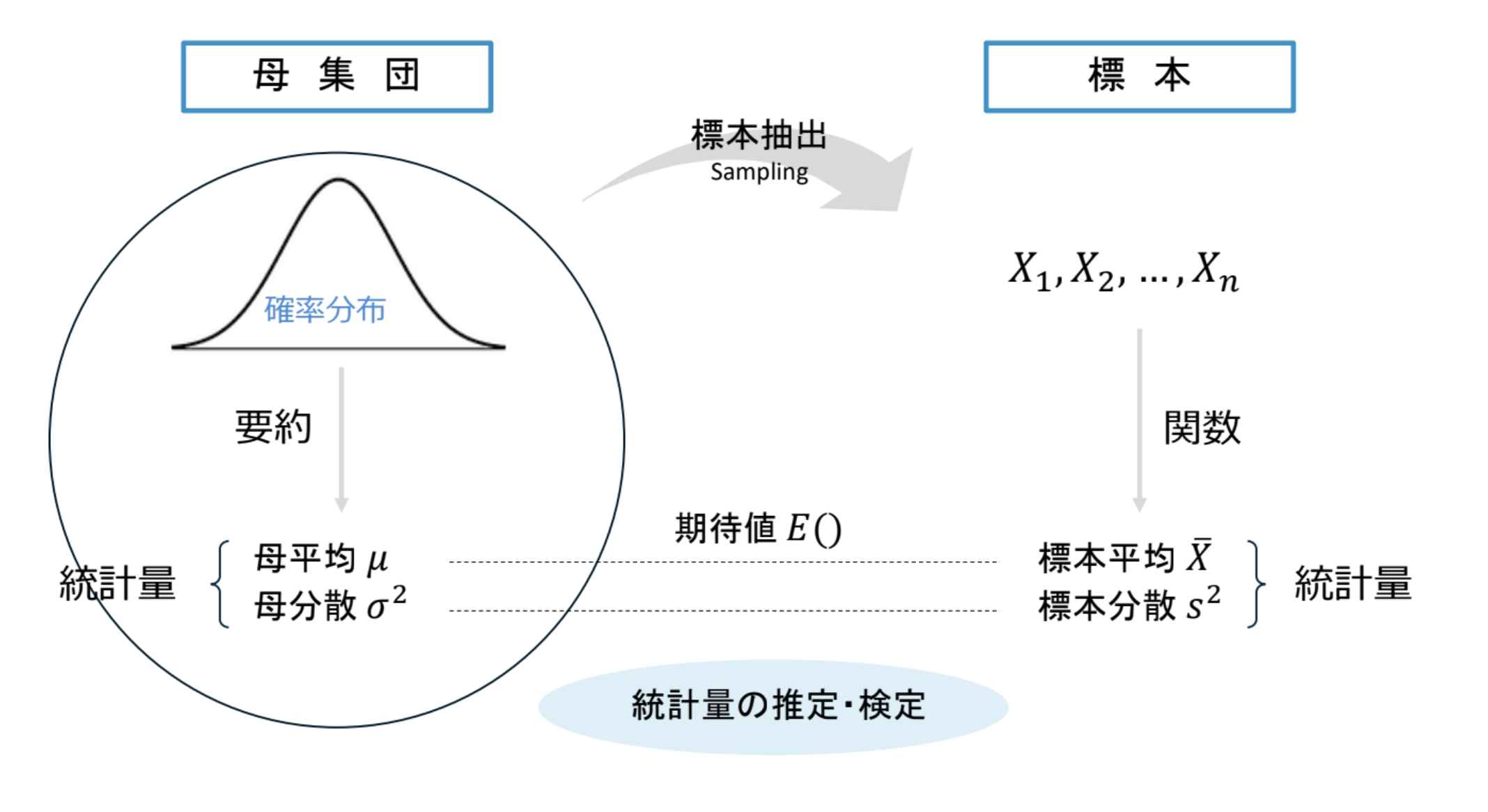



4 標本分布とその近似 Bootcamp For B4




Pythonで実装する確率モデル 標本空間 確率変数 確率分布 スクラッチ実装で理解する基礎統計 3 Liberal Art S Diary
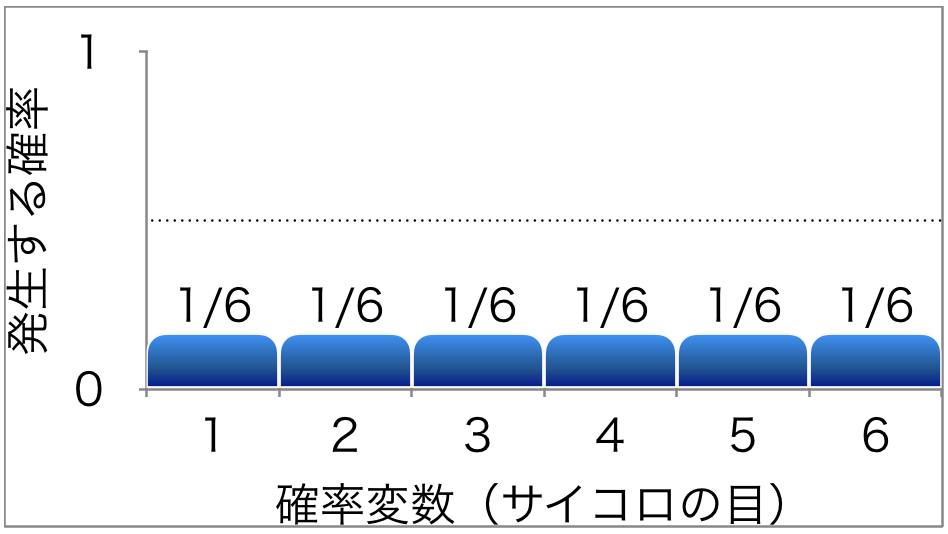



確率変数と確率分布を使ってベストな選択をする方法
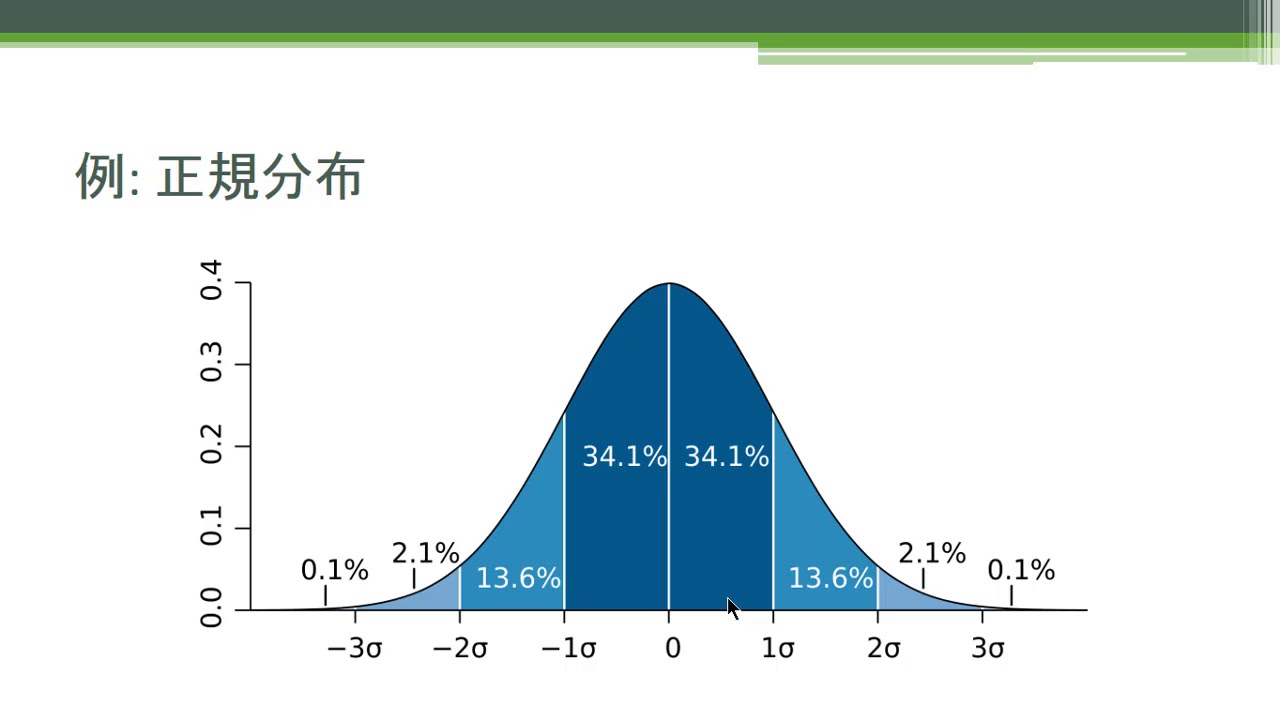



実践データサイエンス 機械学習 With Python 確率密度関数と確率質量関数 Youtube




確率密度関数 Wikipedia




Pythonで主要な確率分布に従う乱数のヒストグラムと確率密度関数のグラフ描画 Santakalog



確率変数 確率分布 確率密度関数とは 制御工学の基礎あれこれ




統計と確率 確率分布
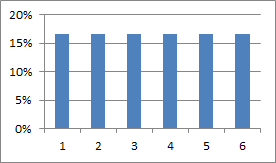



情報処理技法 統計解析 第7回
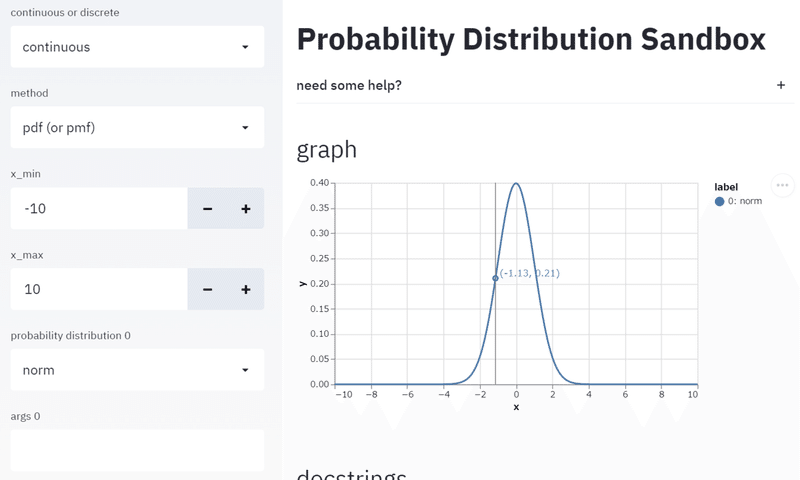



様々な確率分布を可視化するwebアプリの紹介 ガチャのシミュレーションに便利 Dr666m1 Note



確率分布 確率 統計 web教材 木暮



S軌道とp軌道の確率分布曲線を説明できますか Quora




連続および離散確率分布 Minitab




正規分布 Wikipedia
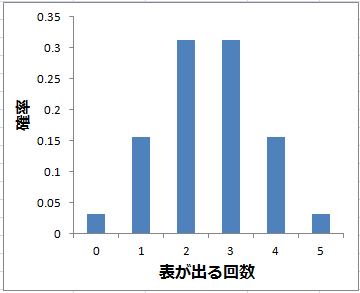



情報処理 第5回 連続確率分布




離散型 連続型確率分布 Ssk Communications



1




確率分布の使い方 正規分布 データ分析教室 Nava ナバ




データ解析 マイニングとr言語



第2回 統計数理講座 確率分布 確率と確率変数 基礎から分かる統計学
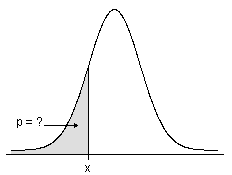



確率分布の方法と計算式 Minitab
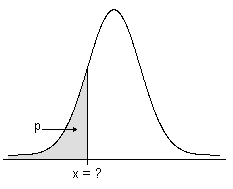



確率分布の方法と計算式 Minitab
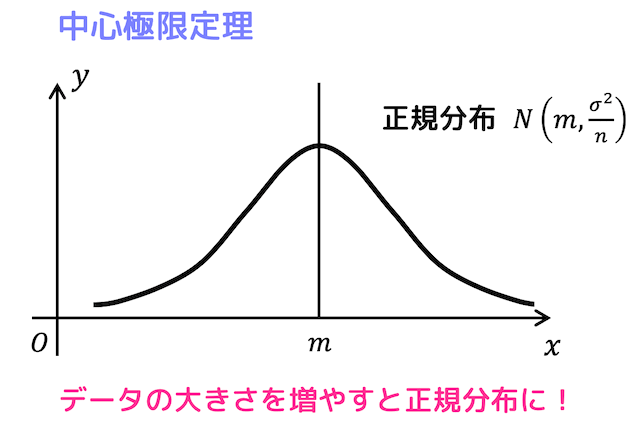



1週間で完成 うさぎでもわかる確率分布と統計的な推測 6日目 母平均 母比率の推定 工業大学生ももやまのうさぎ塾
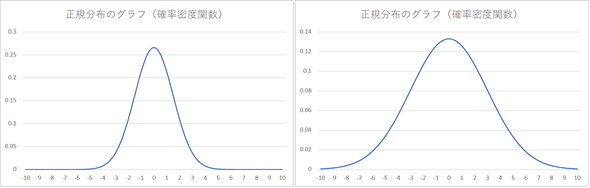



Ai 機械学習の数学 正規分布とベータ分布 確率分布とベイズ統計の関係を理解する Ai 機械学習の数学入門 It




結合確率分布 Blue2718 S Misc
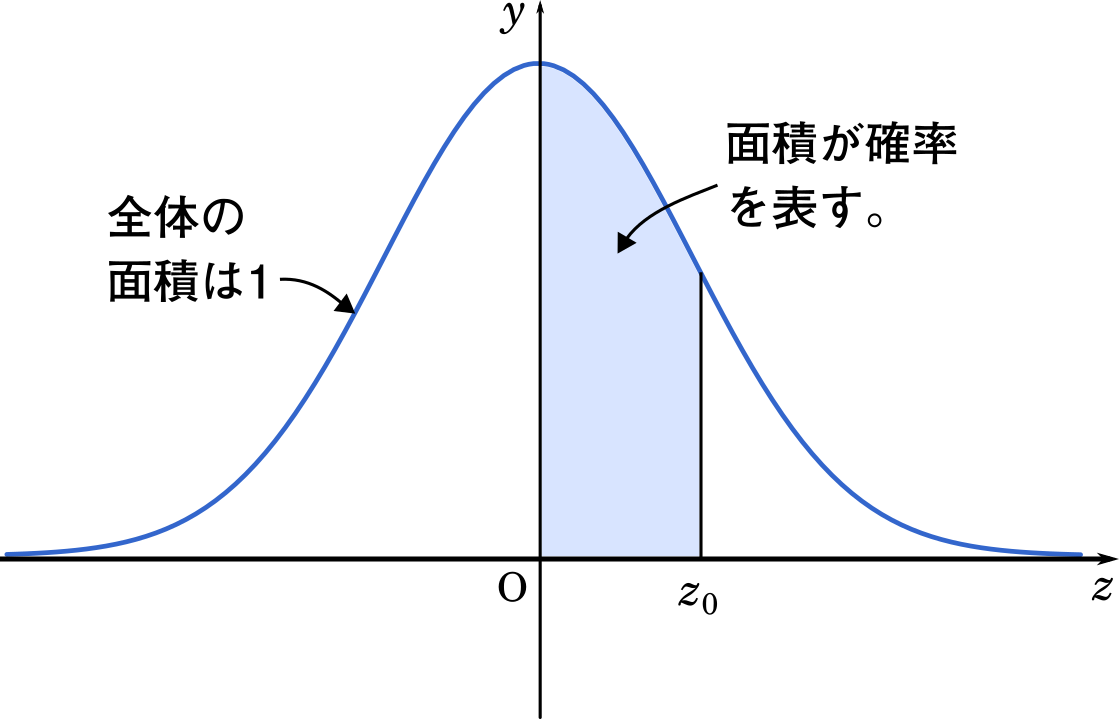



数iib確率分布と統計的な推測 二項分布を標準正規分布にするときの考え方 Mm参考書



同時分布 統計ブログ



確率分布 Excel
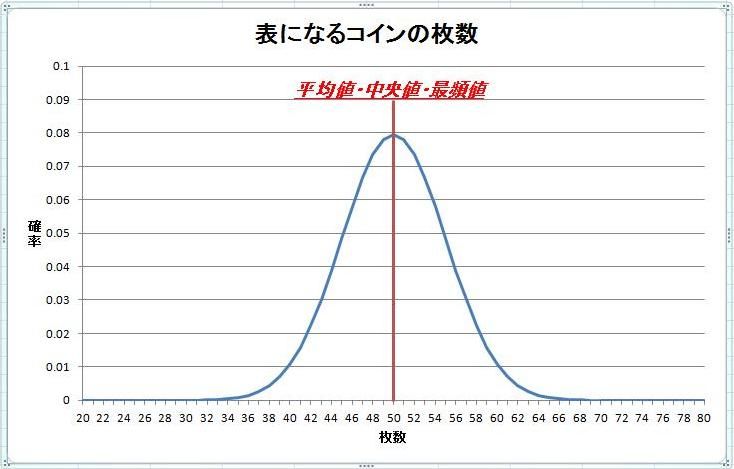



確率分布と平均値 中央値 最頻値 麻雀記 かずっち




統計検定2級対策 確率変数と確率分布 Program As Life




確率分布の使い方 正規分布 データ分析教室 Nava ナバ




確率分布の基本 正規分布について5分でざっくり理解できる記事 Np Urのデータ分析教室



確率論




代表的な確率分布の特徴まとめ Qiita




初心者からはじめる統計学



確率分布を学ぶための基礎知識 Juki Note




問題14 全部 確率分布ノート 解説動画 チャート式の数研出版




確率密度が1を超えるのはおかしいか クイックノート




号 日射量出現確率分布解析法 日射量出現確率分布解析システムおよび日射量出現確率分布解析プログラム Astamuse



音声信号処理の基礎理論 前編 音声圧縮 ノイズ除去 音源分離で用いられる理論 Tech Village テックビレッジ Cq出版株式会社



第5章 確率分布 It情報バンク
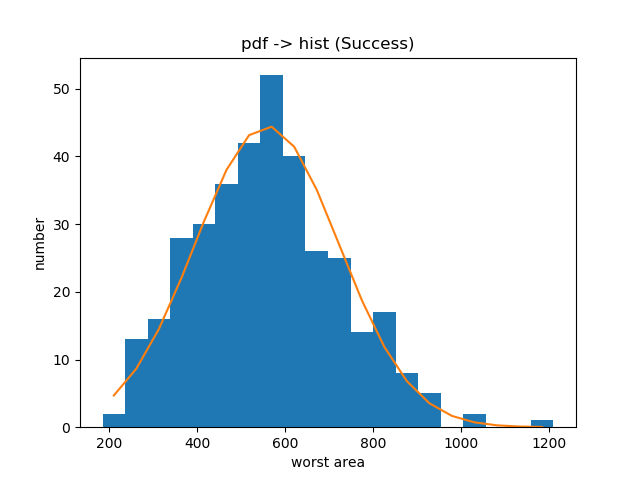



ヒストグラムと確率分布の同時プロット フィッティング精度の検証用に Ushitora Lab




第4回 確率分布 Oac 鬼の居ぬ間に遊ぶ倶楽部



正規分布
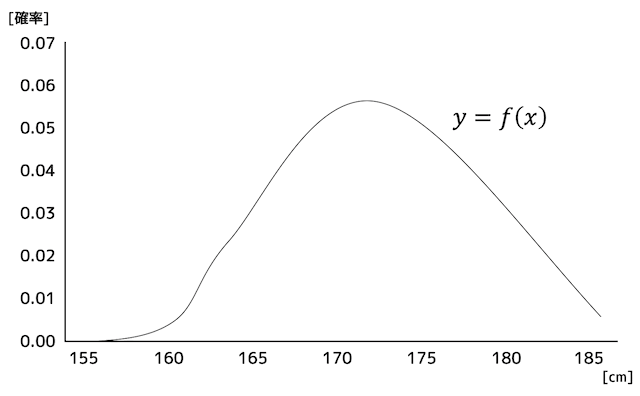



確率統計分野で頻出な確率分布 離散型確率分布編 工業大学生ももやまのうさぎ塾




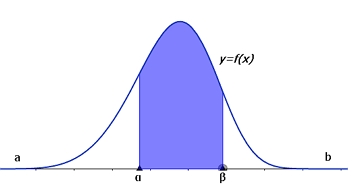
確率と面積の関係 3
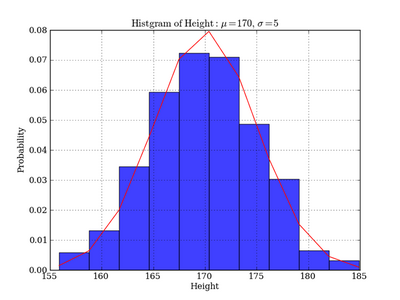



第7回 代表的な離散型確率分布 機械学習 はじめよう Gihyo Jp 技術評論社




確率分布からの乱数の生成1 確率変数の変換 Daily Tech Blog




一変数確率分布関数の基本 確率分布を特徴つける7つの量 努力のガリレオ
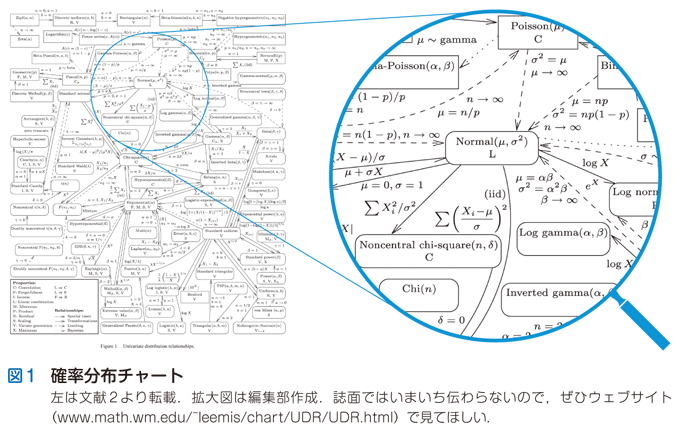



第9回 秘宝 確率分布曼荼羅の発見 統計の落とし穴と蜘蛛の糸 Smart Lab Life 羊土社




正規分布1 準備としてのガウス積分 身勝手な主張



11 4 確率密度と確率密度関数 統計学の時間 統計web




確率母関数で確率分布の特性が求められる マルウェア解析できるデータサイエンティストblog




確率分布 Matlab Simulink Mathworks 日本



高校数学 確率分布と統計的な推測 きのむくままに



Pythonで学ぶ 絶対にわかる確率変数と確率分布と確率密度 データサイエンス入門 統計編18




確率分布 人事のための課題解決サイト Jin Jour ジンジュール



確率論




確率分布とは 高校数学b Youtube



G空間データソリューションセンター
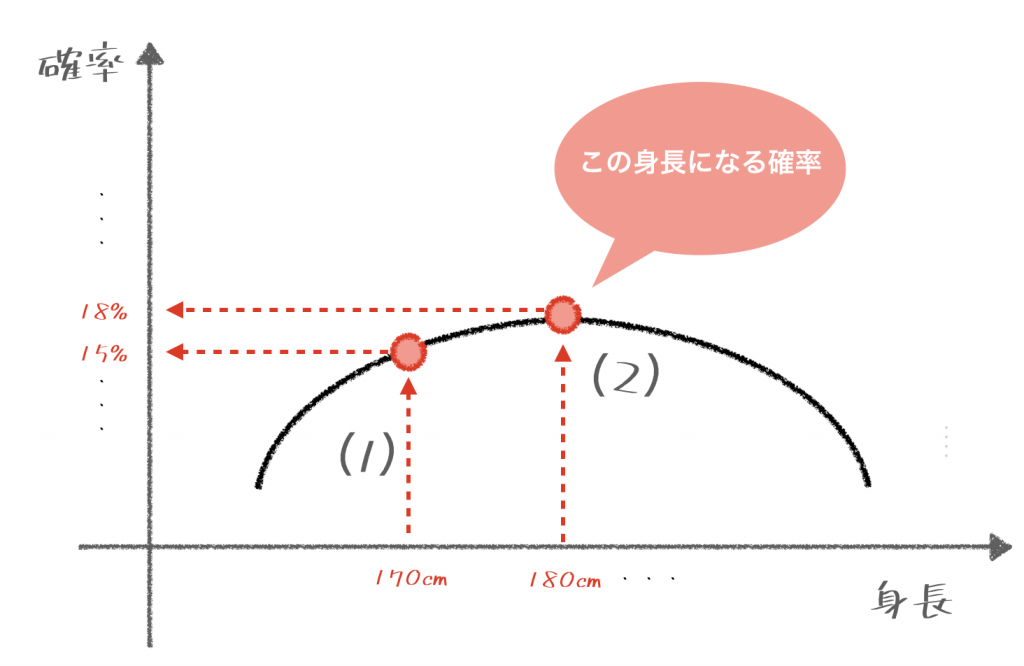



確率分布とは 読み方をやさしく図解 ふわっと理解 小学校の知識でわかる統計辞書




確率分布と統計的な推測 攻略本 センター数学iib第5問を紐解く 朝盈夕虚 Booth




脱統計初学者 確率分布まとめ ベルヌーイ分布 二項分布 ポワソン分布 指数分布 医療職からデータサイエンティストへ
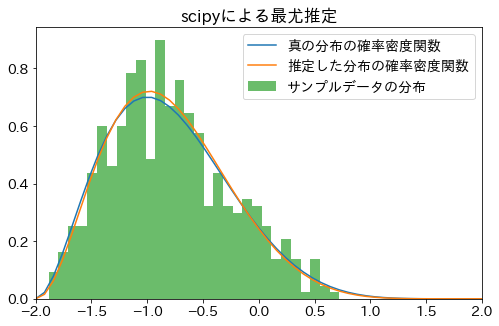



データから確率分布のパラメーターを推定する 分析ノート



確率 確率分布関数 確率密度関数



1



確率分布のベイズ推定




R の 確率密度関数 Rnorm Pnorm Qnorm Dnorm とは何なのか 医療職からデータサイエンティストへ



11 5 連続型確率分布と確率1 統計学の時間 統計web
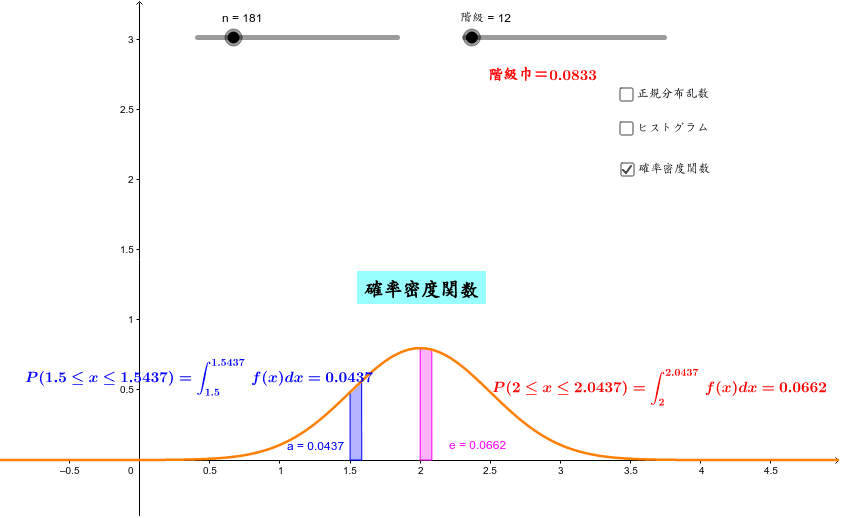



確率密度関数 Geogebra
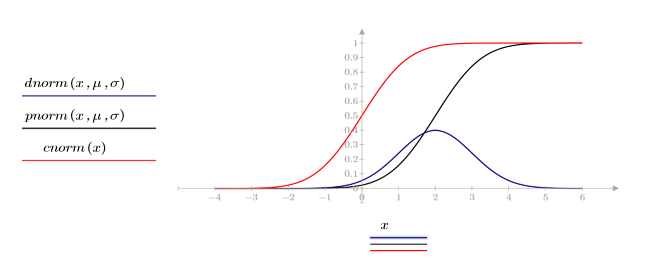



例 確率密度と累積確率分布



確率密度関数とは 連続型確率変数の期待値 分散の求め方 受験辞典
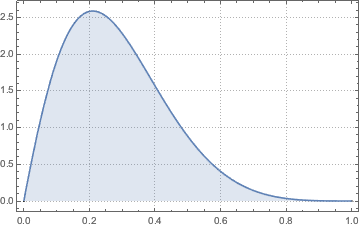



確率変数の積と商の確率密度関数 Wolfram言語 11の新機能
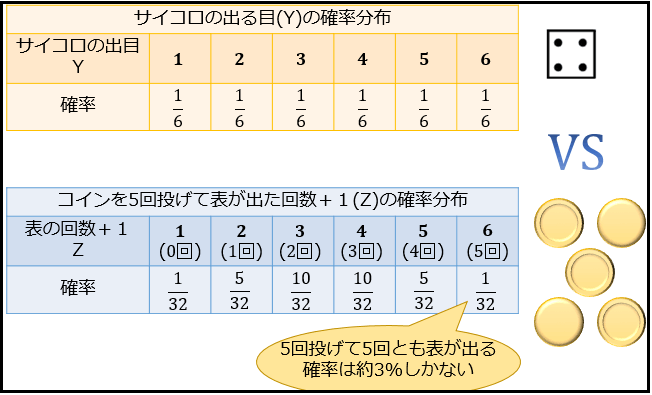



確率変数 確率分布とは何なのか リスクリターン判断の基礎とその有用性について アタリマエ
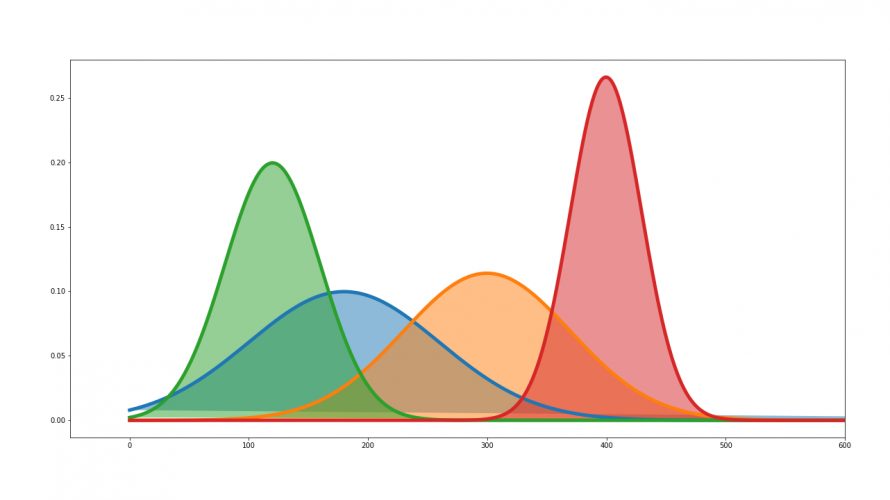



大学のテストや統計検定で頻出の確率分布のまとめ キヨシの命題




多次元の確率分布と確率変数の独立性 確率統計 演習i 17 L06 Youtube
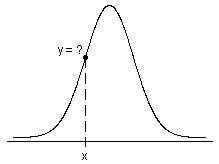



確率分布の方法と計算式 Minitab
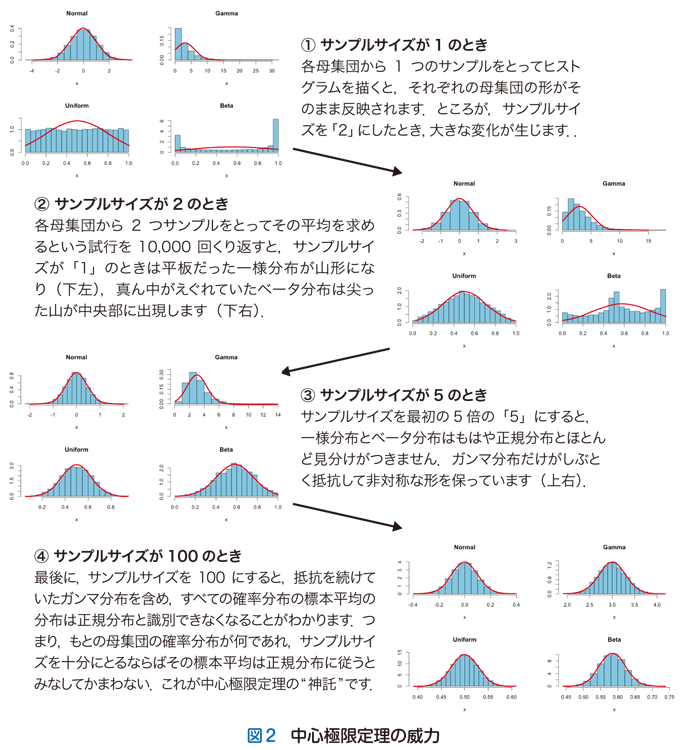



第9回 秘宝 確率分布曼荼羅の発見 統計の落とし穴と蜘蛛の糸 Smart Lab Life 羊土社
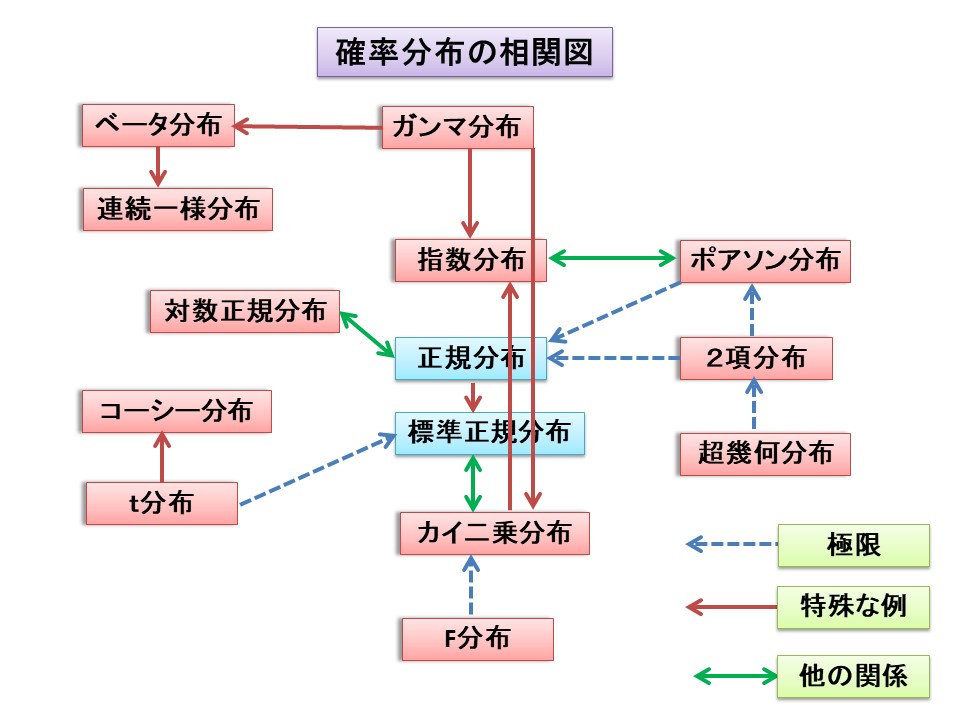



統計検定 公式 V Twitter 確率分布では何が好きですか 正規分布ですか ポアソン分布は人気あると思います 確率分布には生まれた意味もあります お互いの関係は複雑ですが わかると面白いです このサイトは役立ちますよ ブラウザーによって見え方が違い




Scipyで確率分布のサンプルと確率密度関数を生成する 静かなる名辞



Http Www2 Econ Tohoku Ac Jp Terui Lecture Statistics Chapter2 Pdf



14 1 正規分布 統計学の時間 統計web
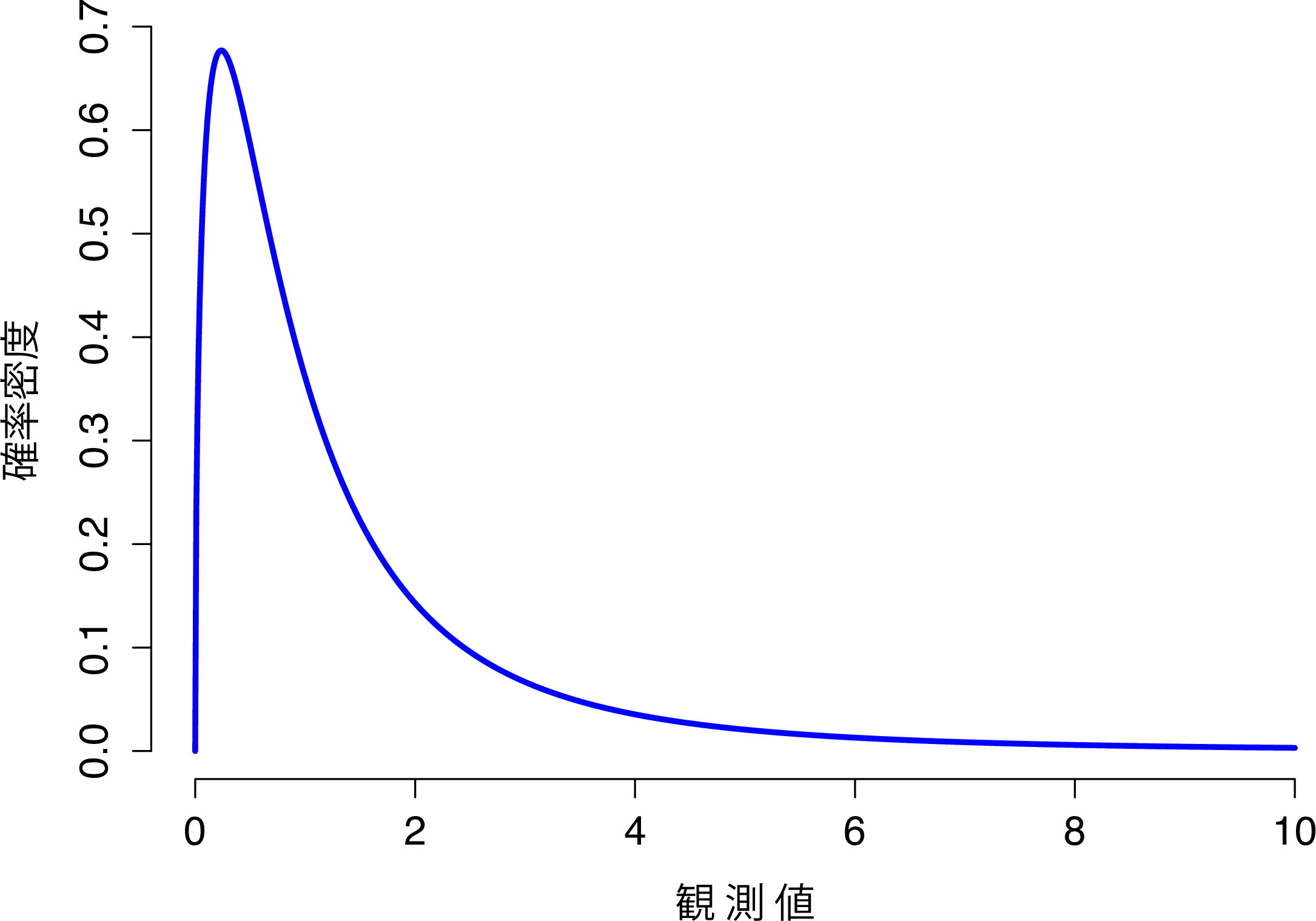



第7章 確率入門 Jamoviで学ぶ心理統計
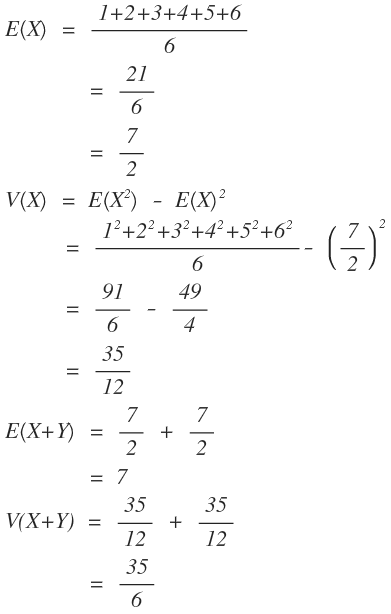



りんだろぐ Rindalog 同時確率分布の期待値と分散の算出法
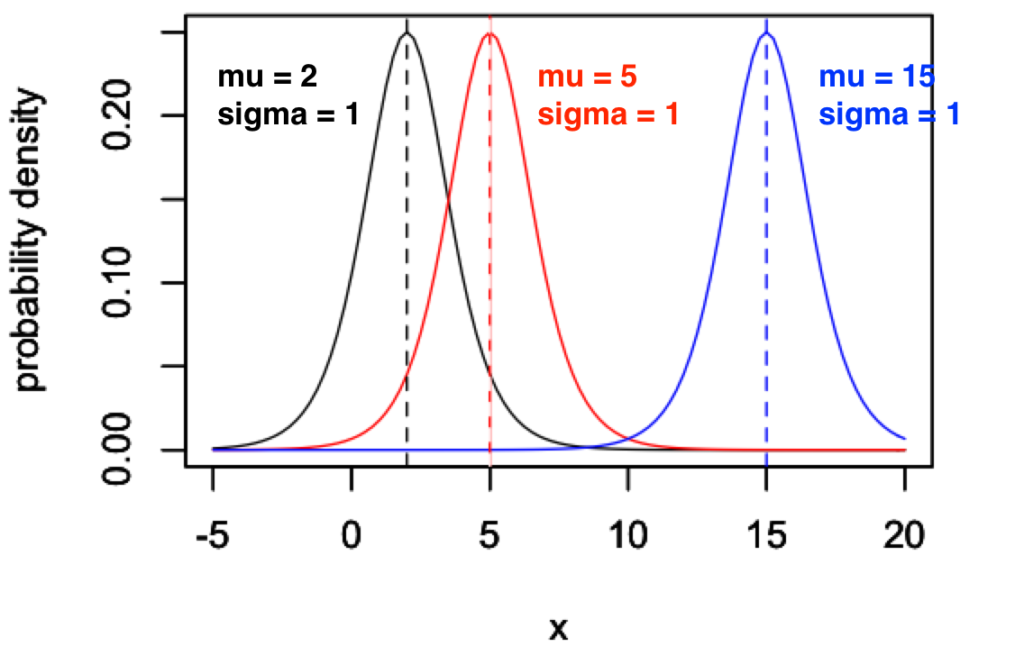



ロジスティック分布は左右対称の確率変数の分布 正規分布に似ています Mi Chan Nel みっちゃんねる



0 件のコメント:
コメントを投稿