図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
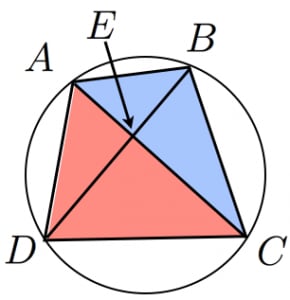
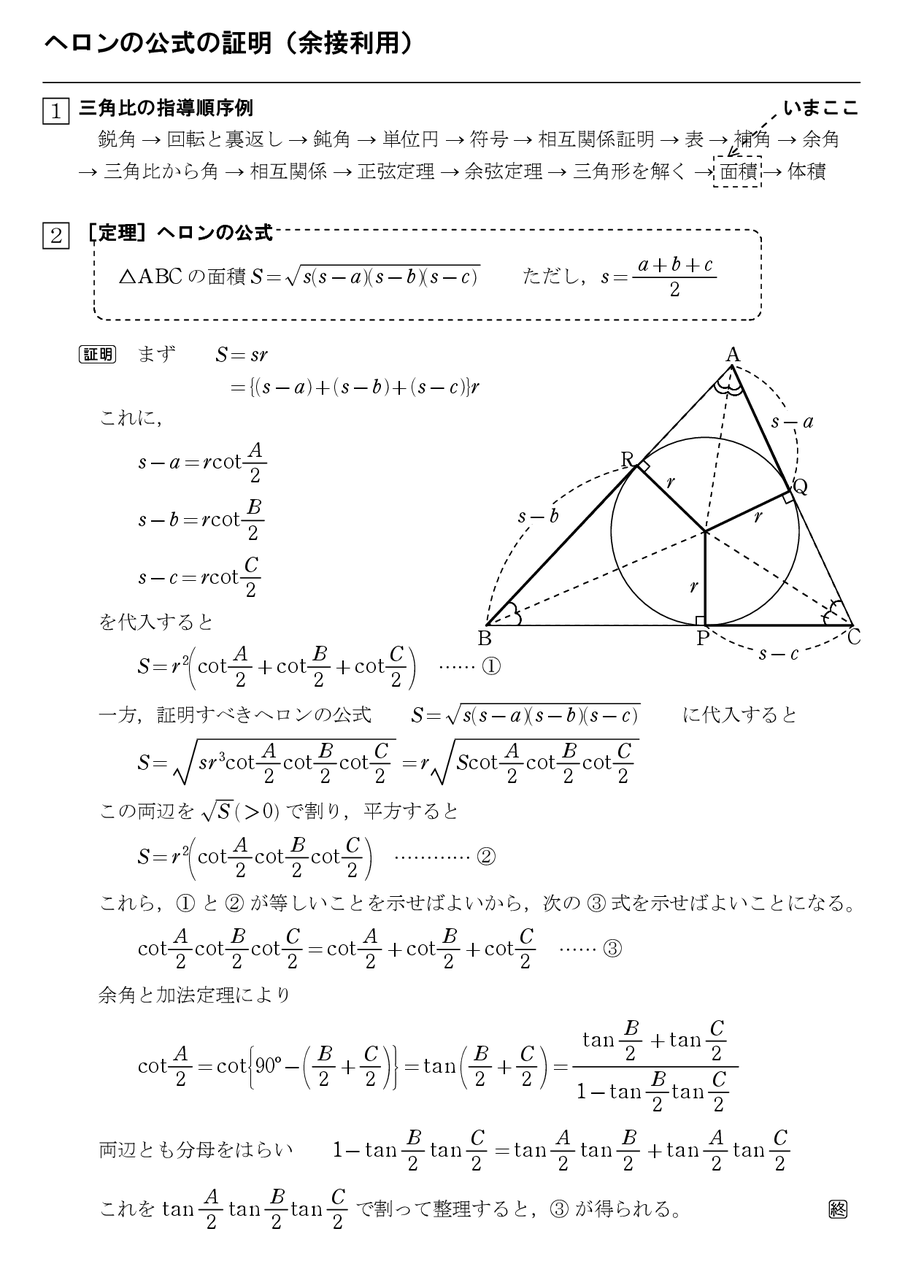
四角形を 2 つの三角形に分けて 、三角形の面積の公式「 \displaystyle S = \frac {1} {2} bc \sin \mathrm {A} 」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。 証明 （見切れる場合は横へスクロール） \angle \mathrm {ABC} = \theta とおくと、 \angle \mathrm {ADC} = 180^\circ − \theta と表せる。 S = 1 2 r ( a b c) S=\dfrac {1} {2}r (abc) S = 21 r(a b c) と似た公式が傍心に対しても成立します。 公式というより考え方が重要。
四角形の面積の公式 高校
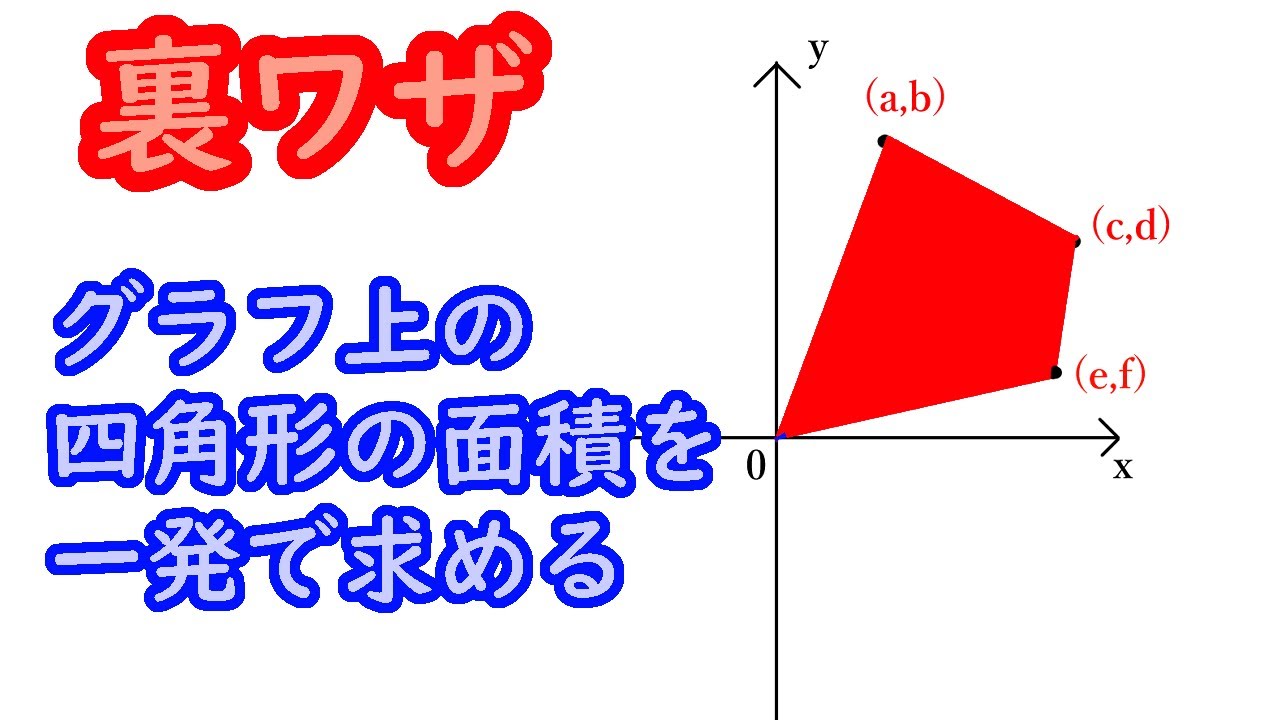
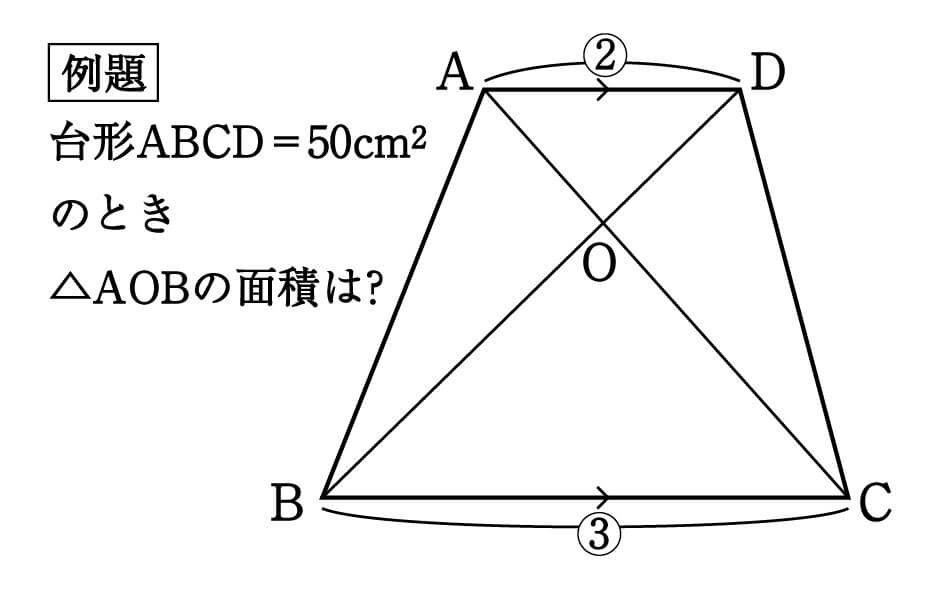
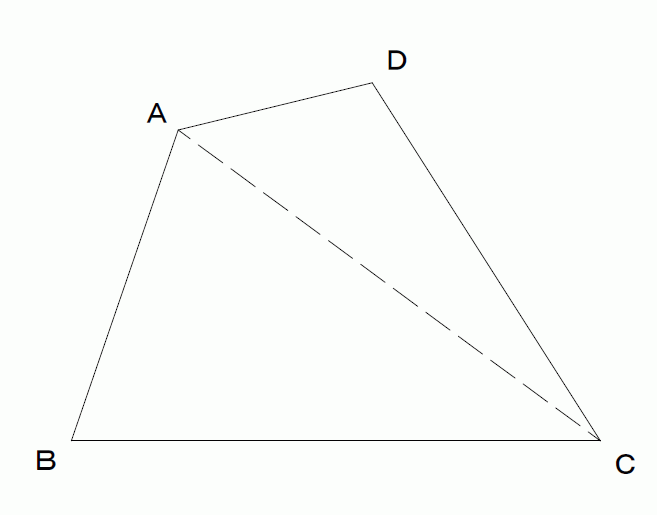
四角形の面積の公式 高校-今回のテーマは「四角形の面積と相似」です。「比」の扱いがポイントです。公立高校受験に備え、力試しにどうぞ。入試本番に向けて、経験値を高めてください。 ※関連動画 高校入試 数学高校受験「折り返しに掲載されている「学び」動画をかんたんに発見！逆に言えば，コンピュータの画面上に題意の図を描くことができれば，問いの答えがほぼほぼ求められたことになりそうです ポイントは，題意の四角形の対角線を一本引く ということです・・・例えば，対角線 \(\mbox{AC}\) です
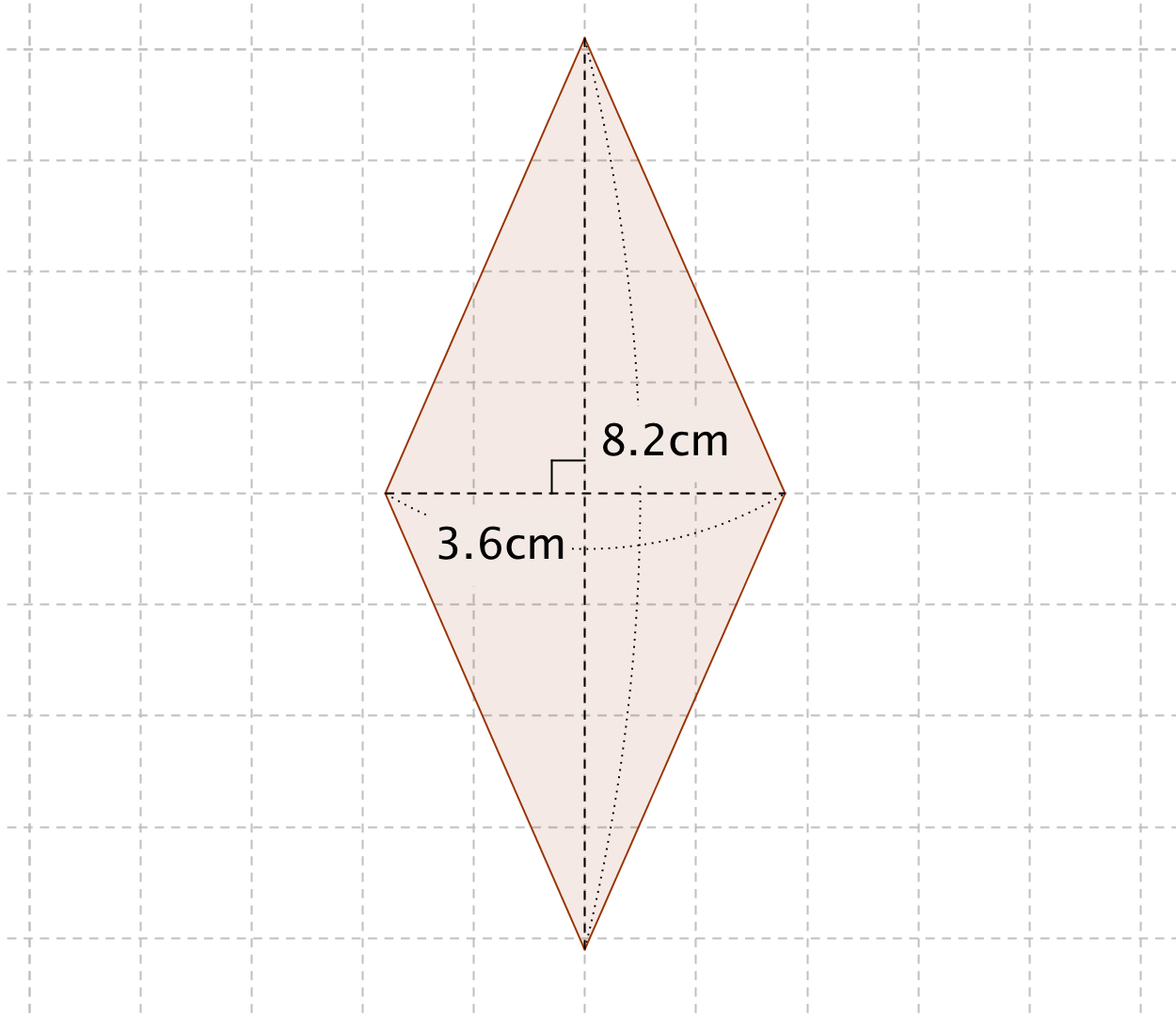
高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月
$3$ 辺の長さと面積がすべて整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼ぶ「ピタゴラスの三角形」(各辺の長さがすべて整数であるような直角三角形)は「ヘロンの三角形」であるよって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり 平行四辺形の面積の求め方 公式と計算例 双心四角形の面積 外接円と内接円の両方をもつ四角形 大学入試数学の考え方と解法 正方形と長方形の面積 家庭学習レシピ 高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかり新潟県 タカ3 さんからの追加問題。 問題1 周長一定の三角形のうち、面積が最大になるのは正三角形である事を証明せよ。 問題2 与えられた円に外接する三角形で、面積が最小になるのは正三角形である事を証明せよ。 (ヒントはヘロンの公式)
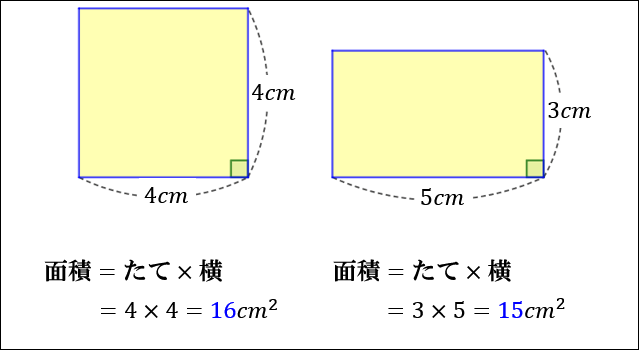
ついては、（一辺）×（一辺）×043の公式は、面積の正確な値ではなく近似値を求める公式となります。 四角形 四角形の面積の公式をご紹介します。 公式の個数は、多角形も合わせて6個になります。前回 https//wwwyoutubecom/watch?v=6MBwzRYm4&index=18&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=cSbY6lb4fng&index 三角形の面積の公式 2辺の長さがa,bでその間の角がθである三角形の面積をSとするとき \( S=\frac{ 数学が苦手な高校生（大学受験生）から数学検定1級を目指す人など，数学を含む試験に合格するための対策を公開 四角形の面積は補助線（対角線）をひい
四角形の面積の公式 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 | 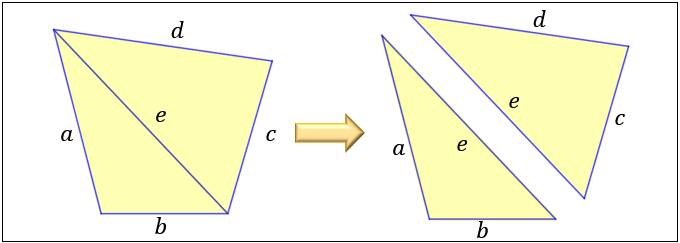3 |
 3 | 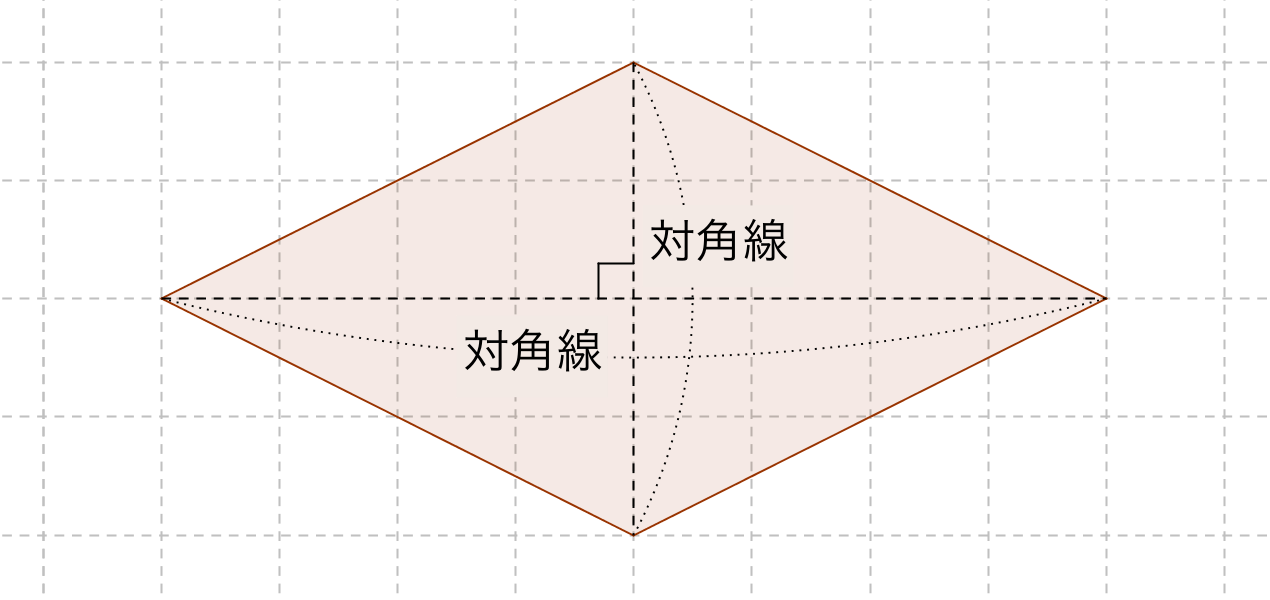 3 |  3 |
 3 |  3 |  3 |
3 |  3 | 3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 | 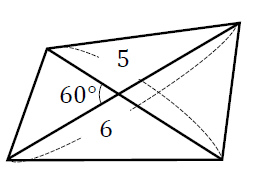 3 |  3 |
 3 | 3 | 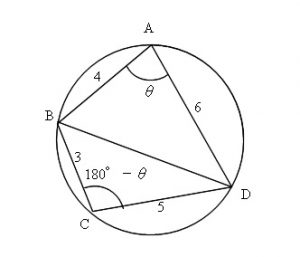3 |
 3 |  3 |  3 |
3 |  3 | 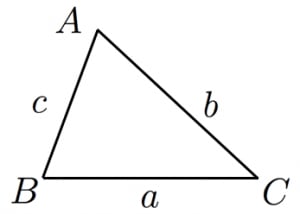 3 |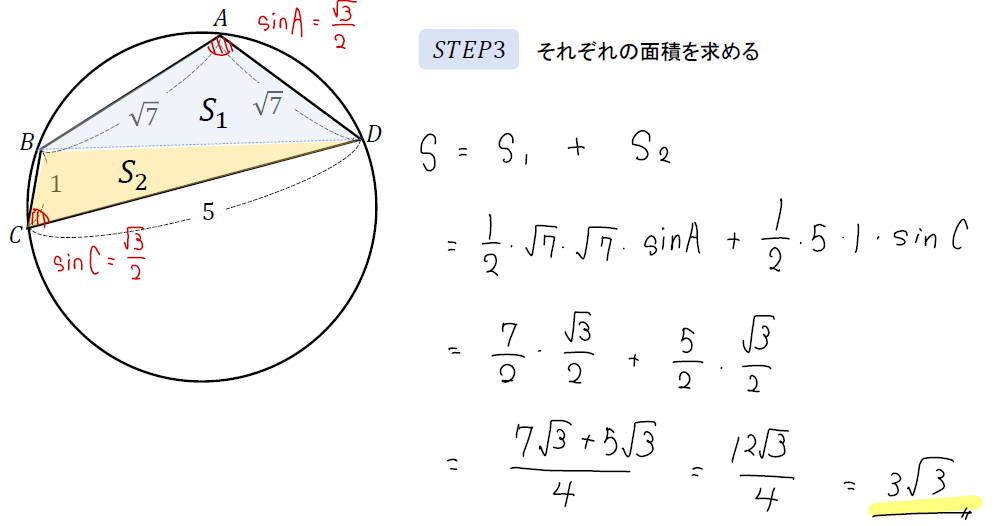
3 |  3 | 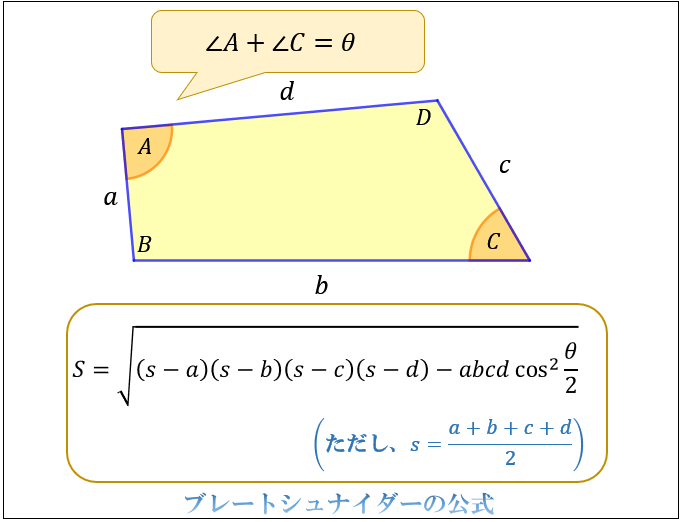 3 |
 3 |  3 |  3 |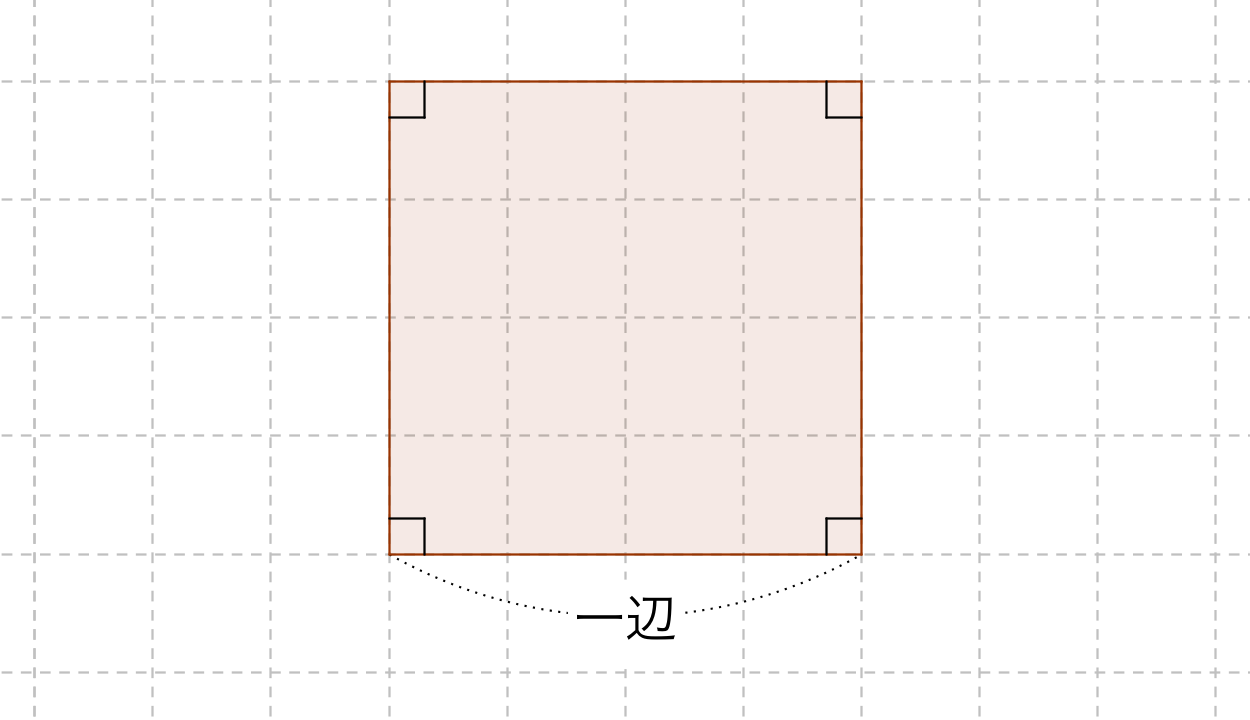
 3 |  3 |  3 |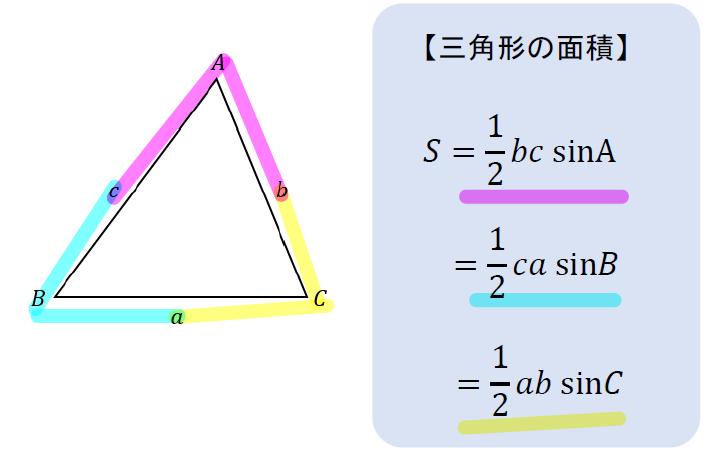
3 | 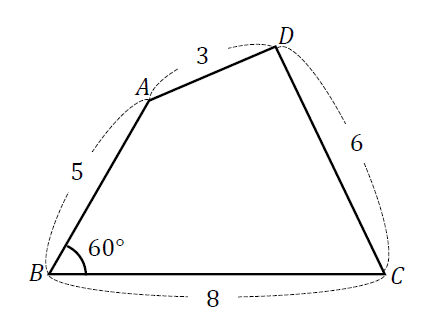 3 |  3 |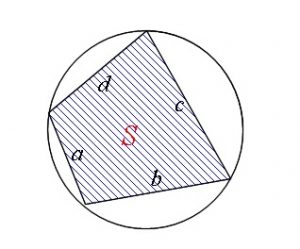
 3 |  3 |  3 |
 3 | 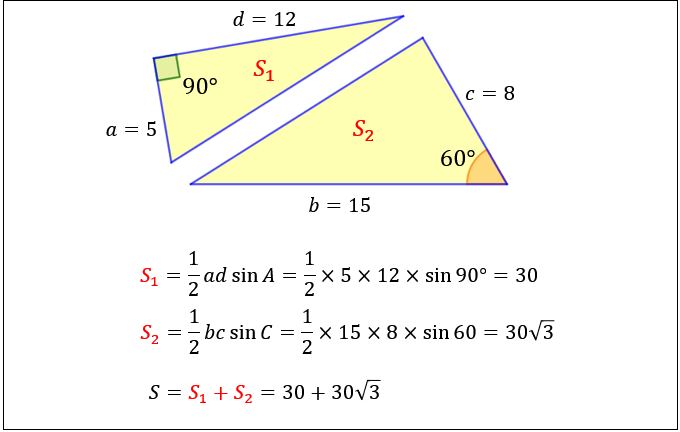 3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |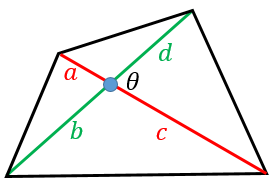
 3 |  3 |  3 |
 3 | 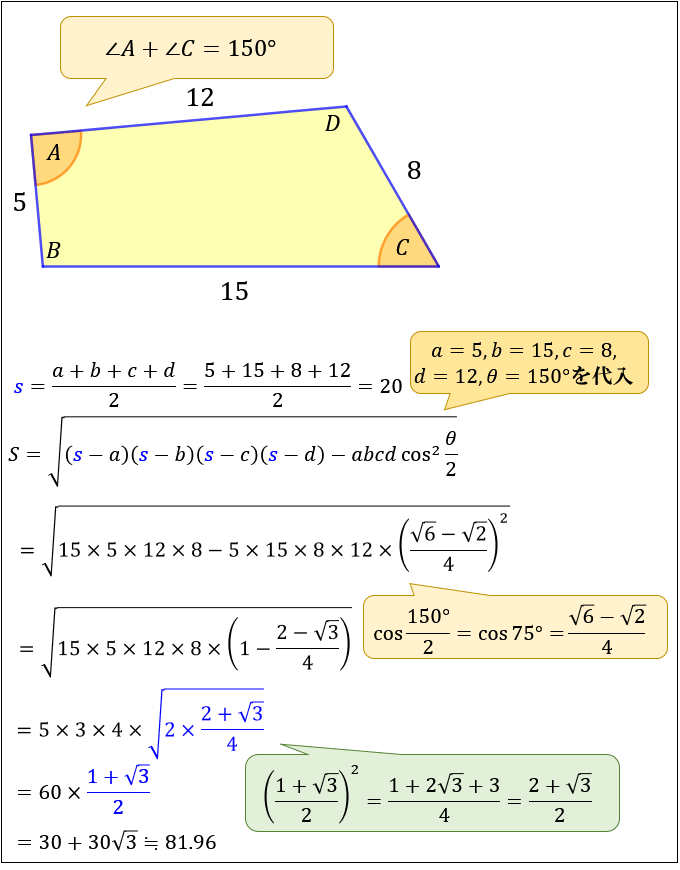 3 |  3 |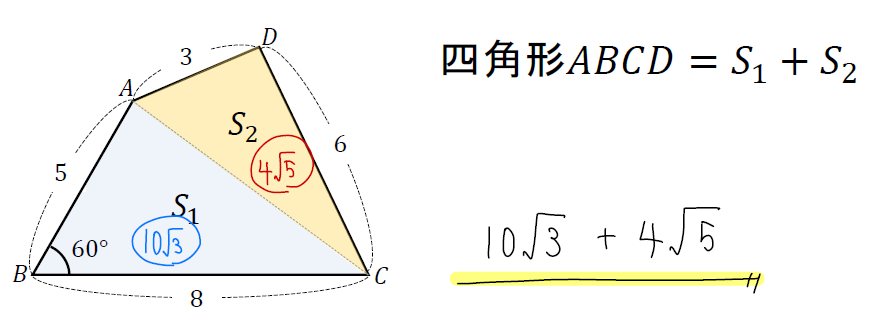
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 | 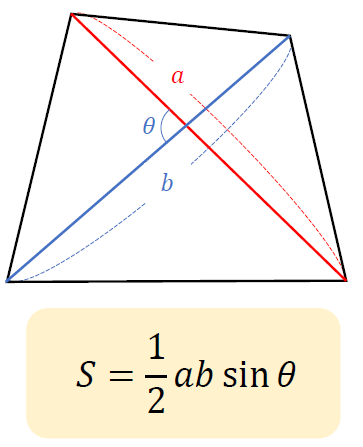 3 |  3 |
 3 |  3 |  3 |
 3 |  3 |  3 |
 3 | 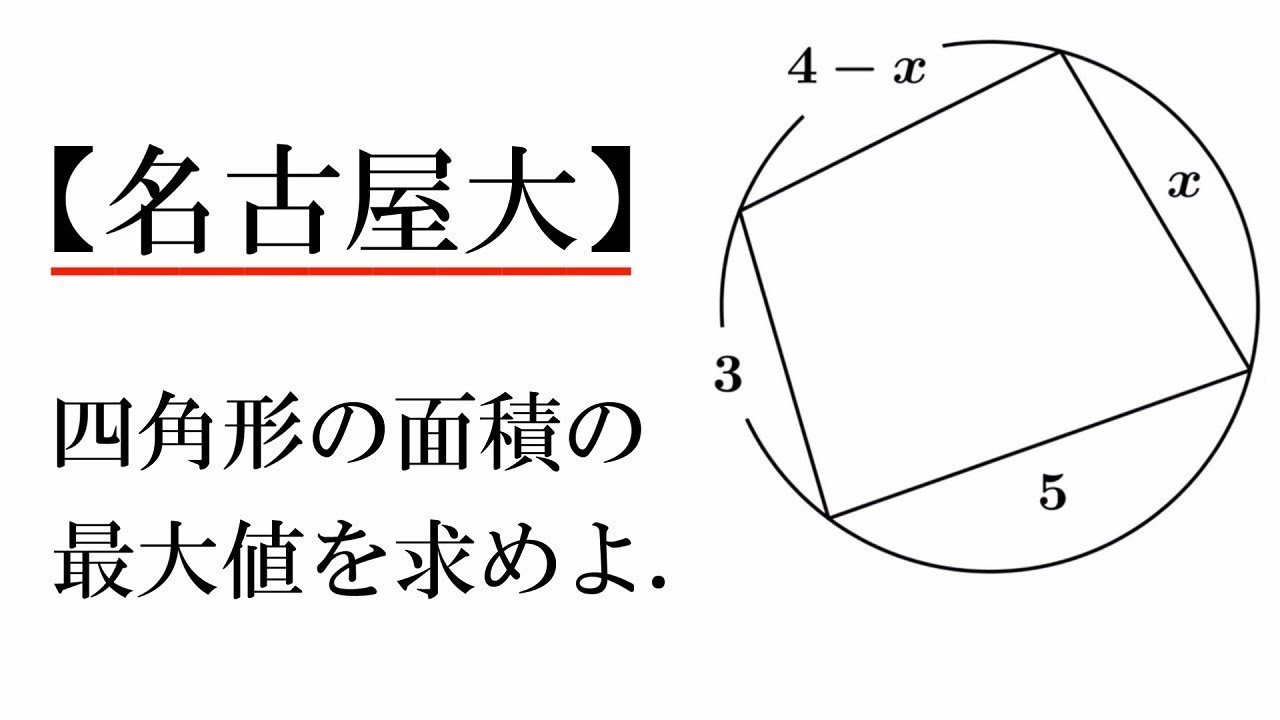 3 |  3 |
 3 |  3 | 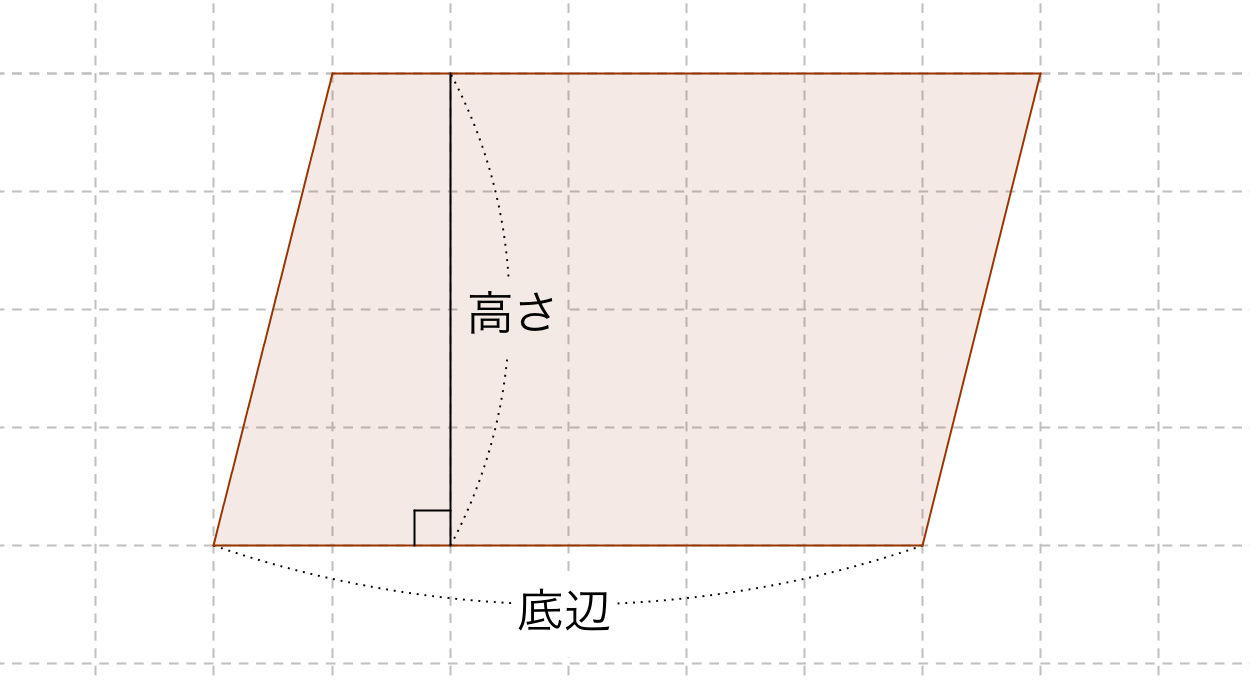 3 |
 3 |  3 | 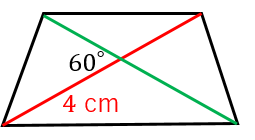 3 |
 3 | 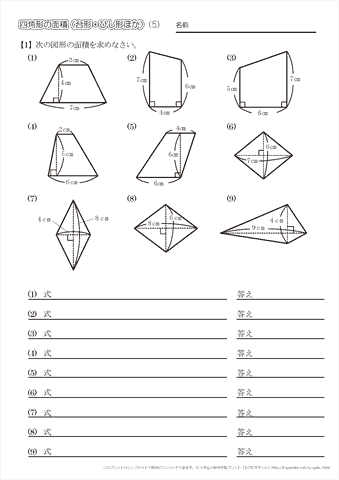 3 |  3 |
 3 |  3 | 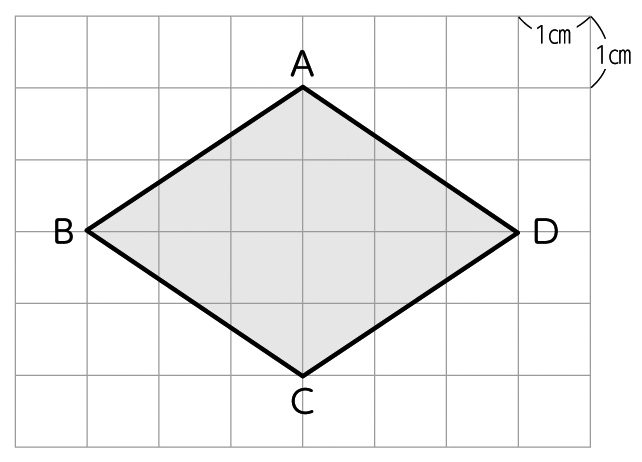 3 |
 3 | 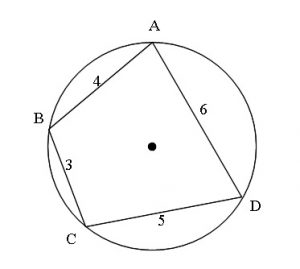 3 |
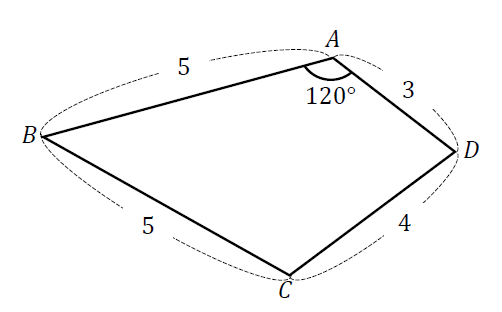
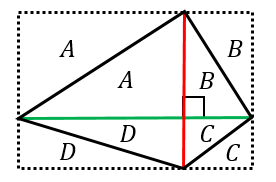
頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b 四角形を2つの三角形に分けてから各三角形の面積 S 1, S 2 を ヘロンの公式 を使って求め、それらを合計することで四角形の面積を求めることができます。 ヘロンの公式 3辺の長さ a, b, c が分かっている場合、その三角形の面積 S は S = s ( s − a) ( s − b) ( s − c) ただし、 ( た だ し 、 s = a b c 2) で求められる。 例題4つの辺 A B = 6, B C = 4, C D = 5, D A = 7, 対角
Incoming Term: 四角形の面積の公式 高校,
0 件のコメント:
コメントを投稿